Просто о саженях и золотой пропорции

Наверняка вы уже имеете какое-то представление о Золотом сечении, я не буду останавливаться на историческом и культурном аспектах — в Интернете полно информации об этом. Я хочу изучить этот феномен с помощью точной науки — математики. В этой статье я покажу, как рождается число Φ, где прячется золотая пропорция и как она применима. А также научу умножать и делить на два. Весь материал является размышлениями на заданную тему — на абсолютную истину не претендует. Призываю вместе проверить всё написанное, математика и геометрия дадут нам ключ.

§1. Начало. Ряд Фибоначчи

Запишем ряд чисел, начиная с единицы, в котором каждое следующее число является суммой двух предыдущих. Найдём отношение каждой пары соседних чисел друг другу, поделив следующее на предыдущее.

1 1 2 3 5 8 13 21 34 55 89

На шестой паре чисел появляется постоянное соотношение 1,618, которое остаётся неизменным до бесконечности, что само по себе уже интересно. Ряд может начинаться с любой пары чисел и соотношение всегда выравнивается до 1,618.

§2. Число Фи

1,618033988749894848045…

Φ — бесконечное иррациональное число. Для наших примеров такая точность не нужна, достаточно 1,618.

§3. Золотая пропорция

Золотое сечение определяют как отношение меньшего отрезка к большему отрезку, как отношение большего к их сумме:

Термин «Золотое сечение» я считаю не совсем корректным, не отражающим процесс. По-английски golden ratio дословно: золотое соотношение. Более уместен термин «Золотая пропорция».

§4. Метрическая система

Так гласит официальное определение метра, принятое XVII Генеральной конференцией по мерам и весам в 1983 году. Метр был введён в СССР 14 сентября 1918 указом СНК РСФСР «О введении международной метрической десятичной системы мер и весов».

Расстояние, пройденное светом за одну трехсотмиллионную долю секунды. Понятно? Как это применять в обычной жизни? Как проектировали и строили сооружения в более ранние века? Неужели мужик, строя дом, будет руководствоваться иррациональными числами и вычислять квадратные корни? Конечно же нет. Очевидно, что существовала другая система мер, и её отголоски сохранились в Королевской системе мер, а также в русских саженях. Нужен простой и понятный инструмент пропорционирования и соизмерения.

§5. Пропорции квадрата

Мы знаем, что у квадрата все стороны равны. А это значит, что квадрат можно нарисовать или построить, имея в руках лишь одну меру любой длины: карандаш, палку и т.д. Примем его сторону за единицу.

Диагональ квадрата — редко используемая величина, но она весьма полезна и интересна (рис. 1).
По теореме Пифагора длина диагонали квадрата (она же гипотенуза треугольника) равна корню из суммы квадратов катетов:

√ (1·1+1·1) = √2 = 1,4142

Пропорцию 1 : √2 также называют серебряным сечением. Самый известный пример этой пропорции — лист формата А4. Эта пропорция обладает интересным свойством, что сохраняется неизменной при удвоении какой-либо из сторон.

Что собой представляет корень из пяти √5 в формуле Φ = (1 + √5) ÷ 2? Это диагональ двух квадратов (рис. 2)! Проверим по теореме Пифагора:

√(1·1+2·2) = √5 = 2,236

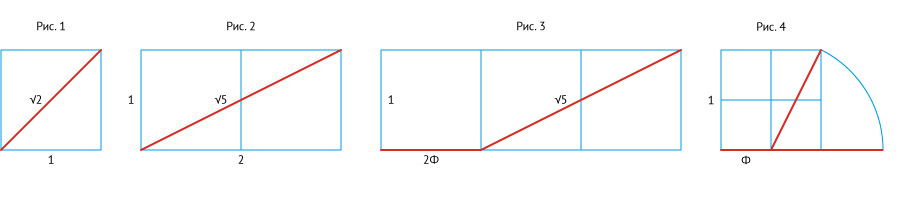
Суммируем величину стороны квадрата (1) и диагональ двух квадратов (2,236). Поделим пополам и получим число Φ. Получается, что длина стороны квадрата и длина диагонали двух квадратов в сумме равны удвоенному числу Φ (рис. 3)!

Φ = 3,236 : 2 = 1,618

Удвоенный квадрат по своей сути также является половиной квадрата большего размера. А значит √5 — это также диагональ половины квадрата, а число Φ можно получить, опустив диагональ половины квадрата на продолжение его стороны (рис. 4).

Квадрат хранит число Φ!

Нам не нужно знать иррациональные числа, математика лишь подтверждает расчёты, но не является их основой! Квадрат хранит в себе все нужные нам пропорции. Он инструмент пропорционирования! Умножая эти пропорции квадрата на целый коэффициент, мы можем получить пропорциональные величины любой нужной длины.

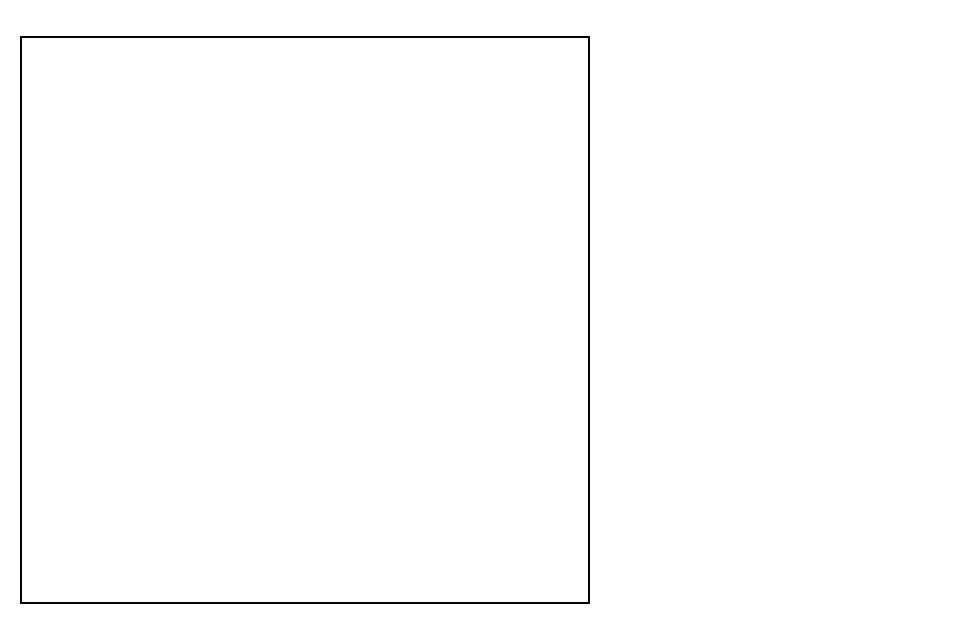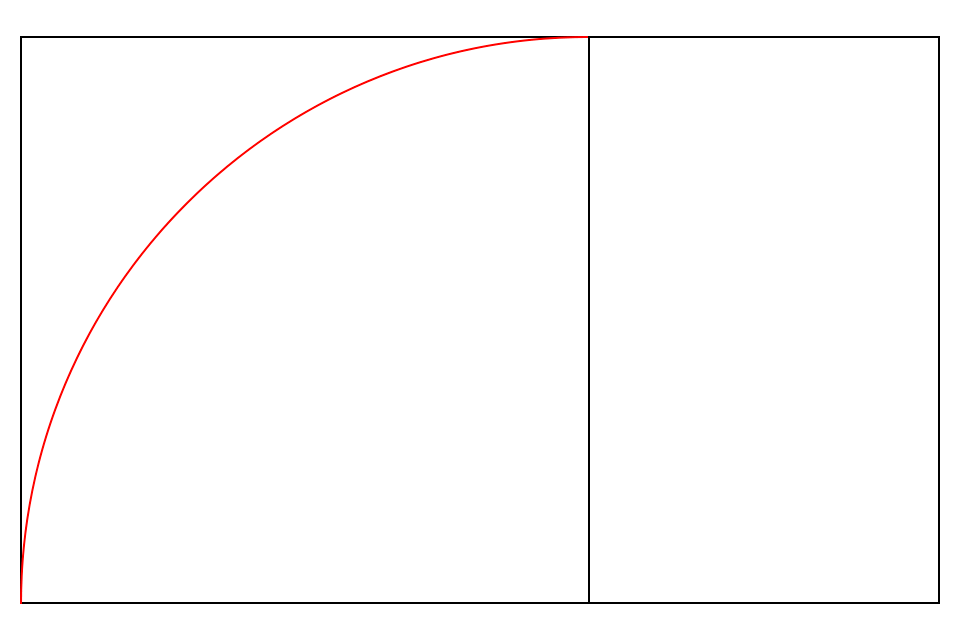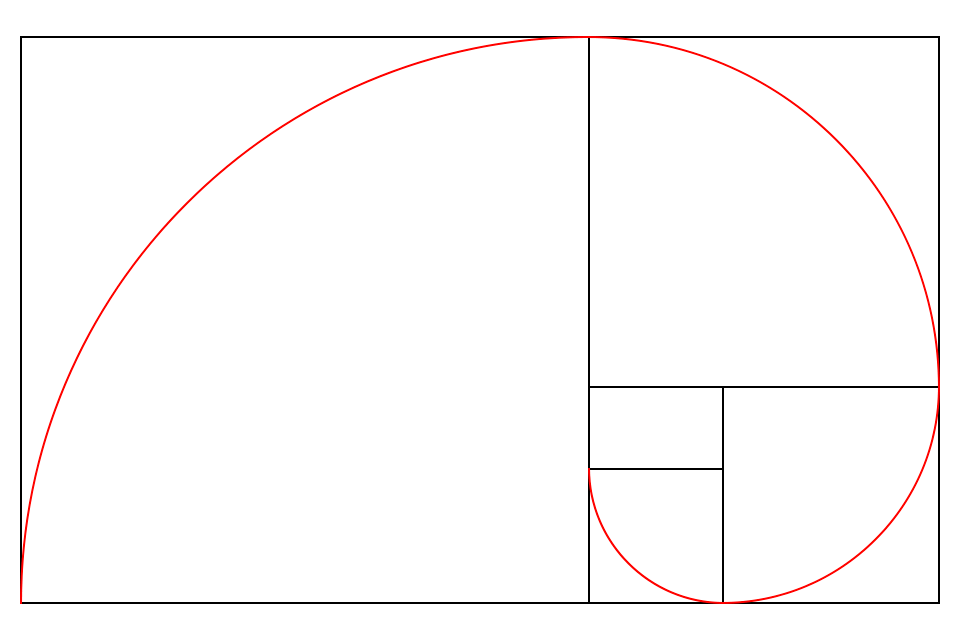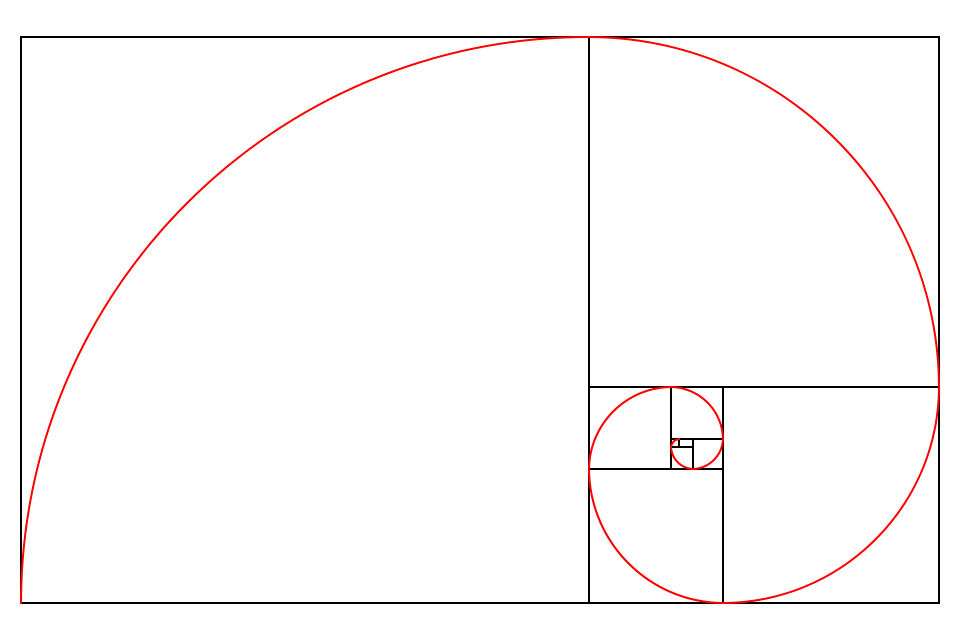
§6. Интересные превращения числа Φ

Теперь стало понятно, где прячется число Φ, я покажу, как оно меняется с точки зрения математики — здесь очень много волшебных превращений! Все они пригодятся нам в дальнейшней работе с саженями.

1). Если от Φ отнять единицу, получится тоже самое, если единицу поделить на Φ:

Φ − 1 = 1 ÷ Φ = 0,618

2). Если из 2Φ вычесть диагональ двух квадратов, получим единицу (рис. 2, 4):

2Φ − √5 = 1,000

3). Помним, число Φ равно половине суммы стороны квадрата и диагонали двух квадратов:

Φ = (1 + √5) ÷ 2 = 1,618

4). Если Φ умножить на диагональ двух квадратов минус единица, будет 2:

Φ · (√5 − 1) = 2,000

5). Если к Φ прибавить единицу, получится тоже самое, если Φ умножить само на себя:

Φ + 1 = Φ² = 2,618

6). Если к Φ прибавить двойку, получится тоже самое, если Φ умножить на диагональ двух квадратов:

Φ+2 = Φ²+1 = Φ·√5 = 3,618

7). Если двойку поделить на Φ получится тоже самое, если из 2Φ вычесть два:

2 ÷ Φ = 2Φ − 2 = 1,236

8). Если из 2Φ вычесть единицу, получим диагональ половины квадрата (рис. 2, 4):

2Φ − 1 = √5 = 2,236

9). Если удвоить Φ, получим 1 + √5 или 2Φ (рис. 3):

2Φ = 1 + √5 = 3,236

10). Если возвести Φ в куб, получим 2 + √5, а это две стороны квадрата + диагональ двух квадратов:

Φ³ = 2 + √5 = 4,236

Трудно не заметить, две группы чисел с одинаковыми знаками после запятой, и это не спроста!

§7. Система пропорций

Возвращаясь к Золотой пропорции. Суть вовсе не в том, что какой-то отрезок делит какой-то другой. Недостаточно нарисовать спираль улитки поверх фото, чтобы понять, что это означает и как этим пользоваться. Для работы на плоскости нужно два отрезка, а для построения объёма нужны три!

1 — 1,236 — 1,618

Появляется система пропорций 1 : 2÷Φ : Φ, которую уже можно использовать как коэффициенты при соизмерении. Рабочая система состоит из трех отрезков и выглядит так:

§8. Образ, подобие, мера и каравай

С математекой, должно быть ясно. Вспомним, что мы, человеки, созданы по образу и подобию Бога, или нашего Создателя, или Вселенной, или Природы, или чего-либо ещё. Оставим религиозные смыслы и обратимся к геометрии. Подобными в ней назвают фигуры одинаковых геометрических пропорций и свойств. Квадраты, круги и равносторонние треугольники всегда подобны таким же фигурам. А раз мы уже нашли золотую пропорцию в числах Фибоначии и в квадрате, давайте искать её в самих себе!

Тело человека уже хранит в себе образ и подобие — Золотую пропорцию!

Вспоминим русскую народную песенку про каравай:

Как на наши именины испекли мы каравай,
Вот такой вышины (поднимаем руки вверх)
Вот такой нижины (опускаем руки вниз)
Вот такой ширины (раскидываем руки вширь)
Вот такой ужины (сводим руки вместе)
Каравай, каравай, кого любишь выбирай!
Я люблю, конечно, всех, но вот (этих) — больше всех.

Какие движения при этом делают дети? Водят хоровод и показывают руками вышину, нижину, ширину и ужину! Проделайте сами те же движения и вы сразу поймёте, какими мерами показывают высоту, ширину и длину. Эта песенка и есть ключ!

Ключ к системе измерений саженями хранится в русской народной культуре! В простой детской песенке, которую знают все с малых лет. Мерить всё по себе — это правильно, логично и само собой разумеется! Однако, теперь это признак эгоизма — выбросим этот нонсенс из своей головы.

§9. Золотая пропорция тела человека

Рука вверх — это мера высоты (великая сажень),
Размах рук в стороны — это мера ширины (маховая сажень),
Рука вперёд — это мера длины (полсажени длины).

Эти меры являются вашими личными мерами!

Все три меры образуют единую систему соизмерений на основе пропорции 2÷Φ к 1. Разные измерения (длина, ширина, высота) должны мериться своей соответствующей мерой, то есть саженью. И тогда мы можем забыть об иррациональных числах, корнях и прочем, используя вместо них целые количества своих саженей.

§10. Казённая сажень отдельно

Важно отметить, что вопреки официально утверждённой казённой сажени, существовали и другие. И лишь она одна была приравнена к 7 английским футам и позже к 213 см в Российской империи и по другим источникам 218 см в СССР. На то она и являлась казённой. В корне неверно считать, что сажень была одна, как метр. Чтобы понять гармонию, не думайте о метре — это изобретение XIX века, а Вселенная со своими пропорциями вечна. :-)

§11. Погрешность измерений

Я намеренно буду округлять сотые и тысячные доли чисел и подтягивать расчёты под единый вид, так как они заведомо не абсолютно точны. Иррациональные числа не делятся до конца, поэтому не везде удастся получить красивые целые числа. А мы должны увидеть картину в целом, понять всю единую систему, где тысячные доли лишь детали.

Сантиметр — это сотая доля метра, достаточно точно, поэтому предлагаю не использовать миллиметры в своих расчётах, чтобы они не создавали лишний шум. К тому же, тело гибкое и руки можно растянуть ещё шире или поднять ещё выше. Этого делать не нужно, положение должно быть комфортным.

§12. Измерим себя и проверим

Пора проверить всё на себе и удивиться, что всё так и есть. Я мужчина среднего роста, мой размах рук примерно 188 см. Высота поднятой руки примерно 232,5 см. Вытянутая рука вперёд (плюс столько же назад) примерно 152 см. Сначала я измерил всё рулеткой, а потом посчитал на калькуляторе. Меня поразило с какой точностью совпали все цифры.

Здесь мы видим четыре любопытных числа. Где же здесь число 1,618? Да вот же оно:

1,236 = 2 ÷ Φ

0,809 = Φ ÷ 2

1,528 = (2 ÷ Φ)²

0,655 = Φ² ÷ 4

Опишем это словами, чтобы появилось понимание, что всё это значит. Поделив сажень высоты на сажень ширины мы получим пропорцию 1 к 2 ÷ Φ, точно также как поделив сажень ширины на сажень длины. Если поменять местами величины, получится пропорция 1 к Φ ÷ 2. Пропорции остаются одинаковы. А значит мы можем подставлять сюда любые величины и любые значения в сантиметрах!

Калькулятор саженей

§13. Как это применять на практике?

Нужно запомнить и взять себе за правило все три измерения мерить соответствующей им мерой. Так как система из трех мер уже имеет в себе золотую пропорцию, то простое умножение и деление на целые числа даст нам гармоничные соотношения размеров.

Самое простое — это умножать и делить на два. Точно также как мы складываем или разворачиваем чистую простыню после стирки: пополам, еще пополам, и снова пополам, пока не получим компактно свернутую вещь. На этом же принципе строится система мер: сажень — полсажени (1/2)  — локоть (1/4) — пясть (1/8) — пядь (1/16) — вершок (1/32).

Рекомедную почитать

• Комбинаторика в дизайне: цвета
• Летопись вязанного ковра
• Кухонная мебель
  из картона
• Как превратить отходы в ценности